Главная     Каталог раздела     Предыдущая     Оглавление     Следующая     Скачать в zip

Региональная экономика и управление

Гаврилов А.И.

Глава 3. Теории размещения регионального производства

3.1. Теория сельскохозяйственного штандорта Й. Тюнена

Становление теории размещения (локализации) принято связывать с выходом в 1826 г. книги немецкого экономиста Й. Тюнена "Изолированное государство в его отношении к сельскому хозяйству и национальной экономии". Главным содержанием этого фундаментального труда было выявление закономерностей размещения сельскохозяйственного производства.

Исследование Й. Тюнена отличали высокий уровень абстракции, точные формулировки поставленных задач. Он предполагал наличие экономически изолированного от остального мира государства, в пределах которого имеется центральный город, являющийся единственным рынком сбыта сельскохозяйственной продукции и источником обеспечения промышленными товарами. Здесь цена каждого продукта в любой точке пространства отличается от его цены в городе на величину транспортных затрат, которые принимаются прямо пропорциональными весу груза и дальности перевозки.

Й. Тюнен ставит вопрос: какие формы примет при установленных предпосылках сельское хозяйство, и какое влияние на его размещение будет оказывать расстояние от города? Он находит ответ на поставленный вопрос методом сопоставления транспортных затрат на перевозку продукции от места производства до рынка, в результате чего выявляются зоны, наиболее благоприятные (с точки зрения минимизации транспортных затрат) для размещения в их пределах тех или иных видов сельскохозяйственного производства.

Й. Тюнен доказывает, что в рамках сделанных допущений оптимальная схема размещения сельскохозяйственного производства — это система концентрических кругов (поясов) разного диаметра вокруг центрального города, разделяющих зоны размещения различных видов сельскохозяйственной деятельности. Чем выше урожайность (продуктивность), тем ближе к городу должно размещаться производство. В то же время чем дороже тот или иной продукт на единицу веса, тем дальше от города целесообразно его размещение. В результате интенсивность ведения хозяйства снижается по мере удаления от города.

Й. Тюнен выделяет шесть поясов (колец) размещения сельскохозяйственной деятельности, основываясь на условиях ведения хозяйства в своем имении в Мекленбурге (рис. 3.1). Ясно, что при других условиях конкретный состав поясов будет другим, но принцип их чередования сохранится.

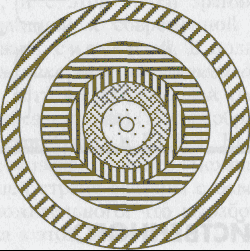
Рис. 3.1. Графическая схема размещения сельского хозяйства по Й. Тюнену

Нахождение расстояния, отделяющего зоны размещения тех или иных видов сельскохозяйственной деятельности от центра сбыта, осуществляется по простым формулам. Пусть имеются "не сельскохозяйственные культуры, доходность которых на единицу продукции составляют т₁и т₂, а объемы их производит" — v₁ и v₂. Транспортный тариф (на 1т) равен t. Тогда r — расстояние от центра, разграничивающее посевы двух культур, находится из уравнения безразличия (равенства разностей между доходом и транспортными затратами):

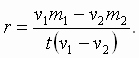
Одновременно Й. Тюнен обосновал основные положения теории земельной ренты по местоположению. Определенный продукт продается по одной и той же цене независимо от места своего производства. Земельная рента равна величине экономии на транспортных издержках в хозяйствах, расположенных относительно ближе к центру. Она максимальна в первом кольце и падает по мере удаления земельного участка от центра. В наиболее удаленном кольце, где еще ведется сельское хозяйство, величина ренты равна нулю. Минимум транспортных затрат на доставку сельскохозяйственной продукции соответствует максимуму земельной ренты.

По-видимому, Й. Тюнен не знал теории ренты по местоположению Д. Рикардо. Тем не менее, начиная свой анализ с принципиально иных посылок, он приходит к тем же выводам, что Д. Рикардо.

Работа Й. Тюнена была первым и весьма показательным пpимером использования абстрактных математических моделей в теории пространственной экономики. Ее важное методическое значение признано в новой экономической науке.

3.2. Рациональный штандорт промышленного предприятия В. Лаунхардта

Главное открытие немецкого ученого В. Лаунхардта,основная работа которого была опубликована в 1882 г., — метод нахождения пункта оптимального размещения отдельного промышленного предприятия относительно источников сырья рынка сбыта продукции.

Решающим фактором размещения производства у В. Лаунхардта, так же как и у Й. Тюнена, являются транспортные издержки. Производственные затраты принимаются равными для всех точек исследуемой территории. Точка оптимального размещения предприятия находится в зависимости от весовых соотношений перевозимых грузов и расстояний. Для решения этой задачи В. Лаунхардт разработал метод весового (или локационного) треугольника (рис. 3.2).

Пусть требуется найти пункт размещения нового металлургического завода. Известны пункт добычи железной руды — точка A пункт добычи угля — точка В и пункт потребления металла — точка С (рис.3.2). Транспортный тариф равен t (на 1 т/км). Расходы руды на выплавку 1т металла составляют: а; расход угля — b. Известны также расстояния между пунктами (стороны локационного треугольника): АС = S₁; ВС = S₂; АВ = S₃.

Возможным пунктом размещения металлургического завода может быть в принципе каждая из трех точек размещения источников руды, угля и потребителя металла. В этих случаях суммарные затраты, связанные с перевозкой всех необходимых грузов для потребления 1т металла, будут равны:

(bS₃ + S₁) t — при размещении завода в точке А;

(aS₃ + S₂) t — при размещении завода в точке В;

(aS₁ + S₂) t — при размещении завода в точке С.

Рис. 3.2. Локационный треугольник В. Лаунхардта

Наилучшим пунктом размещения завода из рассмотренных трех будет тот, в котором транспортные затраты минимальны. Однако искомый пункт размещения может не совпадать ни с одной из вершин локационного треугольника, а находиться внутри него в некоторой точке М.

Расстояние от внутренней точки М до вершин треугольника составляют: AM = r₁ ВМ = r₂ СМ = r_3. Тогда транспортные издержки при размещении металлургического завода в точке М будут равны Т = (ar₁+ br₂ + + r₃) t. Выполнение требования Т → min дает точку оптимального местоположения предприятия.

Данная задача имеет геометрическое и механическое решения. Геометрический метод нахождения точки размещения в том, что на каждой из сторон локационного треугольника строится треугольник, подобный весовому (стороны которого относятся как а : b :1). Затем вокруг построенных таким образом треугольников описываются окружности, точка пересечения которых и является точкой минимума транспортных издержек. Этот метод применим для случая, когда соотношения расстояний S₁, S_2, S₃ соответствуют свойству треугольника (одна сторона меньше суммы двух других). В противном случае (например когда S₁ > S₂ + S₃) точка минимума транспортных затрат будет совпадать с одной из вершин локационного треугольника.

Механическое решение рассматриваемой задачи основывается на аналогии с методом нахождения точки равновесия сил. При этом веса руды, угля, металла выступают в качестве сил, с которыми притягивают производство соответствующие вершины локационного треугольника. Искомая точка является точкой равновесия трех связанных нитей, проходящих через вершины локационного треугольника. При этом к концам нитей подвешены грузы (Q_a,Q_b,Q_c),пропорциональные a, b, 1. Весовой треугольник В. Лаунхардта — одна из первых в экономической науке физических моделей, используемых для решения теоретических ипрактических задач.

Изложенный метод нахождения оптимального размещения предприятия применим и для большего числа точек (видов сырья) при условии, что они образуют выпуклый многоугольник.

3.3. Теория промышленного штандорта А. Вебера

Основной труд немецкого экономиста и социолога А. Вебера "О размещении промышленности: чистая территория штандорта" был опубликован в 1909 г. Ученый поставил перед собой дачу создать общую "чистую" теорию размещения производства на основе рассмотрения изолированного предприятия. Он сделал существенный шаг вперед по сравнению с Й. Тюненом и В. Лаунхардтом, введя в теоретический анализ новые факторы размещения производства в дополнение к транспортным издержкам и ставя более общую оптимизационную задачу: минимизацию общих издержек производства, а не только транспортных.

А. Вебер создал подробную классификацию факторов размещения по их влиянию, степени общности и проявлениям. Фактором размещения он называет экономическую выгоду, "которая выявляется для хозяйственной деятельности в зависимости от места, где осуществляется эта деятельность. Эта выгода заключается в сокращении издержек по производству и сбыту определенного промышленного продукта и означает, следовательно, возможность изготовлять данный продукт в одном каком-либо месте меньшими издержками, чем в другом месте". В результате отсеивания элементов производственных издержек, не зависящих от местоположения, А. Вебер оставляет три фактора: издержки на сырые материалы, издержки на рабочую силу и транспортные издержки. Однако первый из них — разницув ценах на используемые материалы — можно, как считает Вебер, выразить в различиях транспортных издержек, исключив из самостоятельного анализа. Все остальные условия, включающие размещение предприятия, он рассматривает как некоторую "объединенную агломерационную силу", или третий штандортный фактор. Таким образом, в конечном счете анализируются три фактора: транспорт, рабочая сила и агломерация.

Дальнейший анализ ведется последовательно по трем факторам. Соответственно выделяются и три основные ориентации в размещении: транспортная, рабочая и агломерационная.

Транспортная ориентация. Согласно Веберу, величина транспортных издержек зависит от веса перевозимых грузов и расстояния перевозки. Под влиянием транспортных издержек промышленное предприятие будет притягиваться к тому пункту, в котором с учетом местоположения потребительского центра и источников сырья транспортные издержки минимальны. Этот пункт есть транспортный штандорт (транспортный пункт). Для его нахождения используется весовой (локационный) треугольник В. Лаунхардта. При этом важную роль играют два показателя: материальный индекс и штандортный вес.

Например, для производства 100 т продукта требуется 300 т одного материала и 200 т другого. Тогда материальный индекс будет равен (300 + 200) : 100 = 5. Штандортный вес составит 300 + 200 + 100 = 600 (т), или 6 в пересчете на 1т готового продукта, т.е. штандортный вес равен материальному индексу плюс единица. Существуют производства, у которых материальный индекс меньше единицы. Исходя из соотношения указанных показателей легко установить, что производства с высоким материальным индексом тяготеют к пунктам производства сырья материалов, а производства с небольшим индексом ― к центру потребления.

Рабочая ориентация. Далее, учитывая различия в издержках на рабочую силу (рабочих издержек), определяется рабочий пункт, т.е. пункт с наименьшими рабочими издержками. Рабочий пункт будет притягивать производство к себе, в результате чего производство либо останется в транспортном пункте, либо переместится в рабочий пункт. Такое перемещение может произойти тогда, когда экономия на рабочих издержках в данном пункте перекрывает перерасход в транспортных затратах из-за перемещения производства.

Для определения промышленного штандорта с учетом совместного влияния факторов транспортных издержек и рабочей силы А. Вебер прибегает к построениям так называемых изодапан (isodapane), смысл которых заключается в следующем. Приросты транспортных затрат, обусловленные перемещением производства из транспортного пункта в рабочий, увеличиваются с удалением от транспортного пункта, причем более или менее равномерно в любом направлении удаления. Поэтому в каждом направлении должны существовать пункты, для которых приросты транспортных затрат (или издержки отклонения) будут одинаковыми. Линии, соединяющие эти пункты одинаковых издержек отклонения, и называются изодапанами.

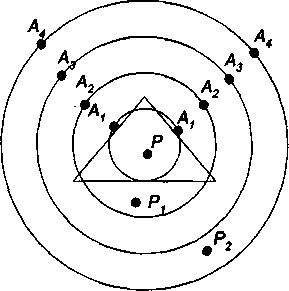
Рис. 3.3. Транспортный и рабочие пункты и изодапаны

Графически (рис. 3.3) такие линии можно представить в виде замкнутых кривых, которые описываются вокруг пункта транспортного минимума (Р)и соединяются точки одинаковых отклонений в транспортных издержках при перемещении пpoизводства в рабочие пункты (P₁ или P₂). При этом изодапана, соединяющая точки, в которых отклонения транспортных издержек равны экономии на рабочих издержках, называется критической изодапаной для данного рабочего пункта.

Если данный рабочий пункт лежит внутри своей критической изодапаны, то перемещение производства из транспортного пункта в рабочий пункт выгодно, а если вне ее, то перемещение невыгодно. Например, если для рабочего пункта P₁критической изодапаной является А₃,то предприятие предпочтительнее разместить в транспортном пункте Р. Если критической изодапаной является А_4, то предприятие целесообразно разместить в рабочем пункте P_1.

Агломерационная ориентация. Анализ влияния агломерационных факторов на размещение промышленного предприятия Вебер провел на базе оценки изменений, вызываемых процессами агломерации, в оптимальной схеме размещения производства, полученной на основе транспортной и рабочей ориентаций. Для этого он ввел дополнительное понятие — индекс сбережений. Смысл этого понятия поясним на следующем простом примере.

Пусть различным объемам агломерированной массы (например, годовым выпускам продукции) соответствуют различные удельные издержки:

1. 100 т — 10 руб.;
2. 400 т — 6 руб.;
3. 1600 т — 4руб.;
4. 6400 т — 3 руб.

Уменьшение удельных издержек при росте объема производства отражает эффект концентрации. Разница в издержках для агломерированных масс по сравнению с первым уровнем концентрации производства составит: для второго уровня — 4(10 - 6); для третьего — 6(10 - 4); для четвертого — 7(10 - 3). Полученные величины (4; 6; 7) и представляют собой те сбережения, которые получаются для различных степеней агломерации и повышаются при укрупнении производства. Эти величины Вебер и называл индексами сбережений при агломерации.

Проводимый анализ влияния фактора агломерации на размещение производства предполагает отсутствие влияния всех других факторов, кроме транспортного. Исходя из транспортной ориентации отыскиваются отклонения производства транспортных пунктов, обусловленные действием фактора агломерации. Такие отклонения целесообразны, если издержки отклонения перекрываются сбережениями в агломерационных пунктах.

Дни определения места размещения агломерационного производства вокруг транспортных пунктов проводятся изодапаны, среди которых выделяется критическая изодапана, т.е. геометрическое место точек, где перерасход транспортных затрат равен экономии от агломерации производства. Вебер утверждает, что отклонение изолированных производств от транспортных пунктов имеет смысл только тогда, когда все отклоняющиеся производства, не выходя за пределы своих критических изодапан, соединятся в каком-то одном месте. Таким местом является площадь общего сегмента, образованного пересекающимися критическими изодапанами, так как только внутри этого сегмента издержки отклонения для каждого производства не превышают той выгоды, которая получается от соединения, т.е. не превышает агломерационных сбережений. Иллюстрацией этого рассуждения является рис. 3.4.

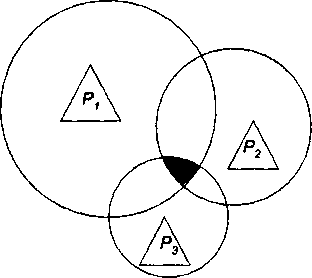
Рис. 3.4. Транспортные пункты и площадь агломерации производств

Агломерируемые производства должны размещаться в штрихованном сегменте. Выбор точки размещения происходит с учетом транспортного фактора. В более общем случае несколько предприятий образуют не один, а несколько сегментов.

А. Вебер рассматривает различные ситуации при осуществлении агломерации, конкретизируя методику нахождения штандорта. Он предлагает формулы агломерационных эффектов.

Пусть М — производственная масса какого-либо крупного производства. Величина сбережений от агломерации в расчете на единицу продукта будет выражаться в виде функции сбережения — f(M). Тогда общая величина сбережений на всю производственную массу составит:

Э₁ = М f(M).

Допустим, что с крупным производством сливается мелкое производство с производственной массой т. Тогда общая суммасбережения для двух производств составит:

Э₂ = (М + т) f(M + т).

Определим приращение сбережения, получаемого в результате слияния двух производств:

Э = Э₂ − Э₁ = (М + т) f(M + т) − M f(M)

Cлияние мелкого производства с крупным происходит, согласно А. Веберу, в том случае, если величина сбережения от слияния предприятий больше (или по крайней мере не меньше) перерасхода транспортных затрат из-за переноса производства т в пункт производства М, т.е.:

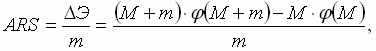
где А — штандортный вес; R — радиус отклонения; S —ставка транспортного тарифа (т/км)

Отсюда можно определить величину наибольшего, экономики допустимого, радиуса отклонения.

Определяем первую производную функции:

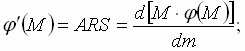
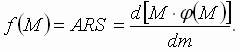
Функция f(M), называемая функцией агломерации, служит выражением притягательной силы крупного производства по отношению к рассеянным мелким производствам. Поскольку f(M) = ARS, то R = f(M) : AS, т.е. максимально допустимый радиус отклонения прямо пропорционален функции агломерации и обратно пропорционален штандортному весу и тарифной ставке.

Выведенная формула агломерации f(M) = ARS включает три фактора, от которых зависит агломерация. Требуется учесть еще одно условие — производственную плотность.

Обозначим через р производственную плотность, под которой здесь понимается объем продукции, приходящейся на единицу площади с радиусом R, при равномерном распределении производства на данной площади. Тогда вся производственная масса, притягиваемая к агломерационному центру, будет равна πR²p = М. Отсюда

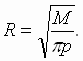
Сравнивая полученную формулу с ранее выведенной, получаем окончательную формулу агломерации

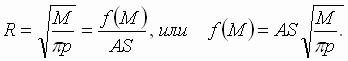
А. Веберу первому удалось выработать многофакторную теорию размещения промышленного предприятия, опирающуюся на методы количественного анализа (математическое моделирование). Так же как и его предшественник В. Лаунхардт, А. Вебер не вышел за рамки проблемы размещения отдельного предприятия. Однако его исследования стали мощным стимулом для создания более общих теорий размещения.

3.4. Теория центральных мест

Первую теорию о функциях размещения системы населенных пунктов (центральных мест) в рыночном пространстве выдвинул В. Кристаллер в своем труде "Центральные места в южной Германии", опубликованном в 1993 г. Теоретические выводы он обосновал эмпирическими данными.

Центральными местами В.Кристаллер называет экономические центры, которые обслуживают товарами и услугами не только себя, но и население своей округи (зоны сбыта). Согласно В. Кристаллеру, зоны обслуживания и сбыта с течением времени имеют тенденцию оформляться в правильные шестиугольники (пчелиные соты), а вся заселенная территория покрывается шестиугольниками без просветов (кристаллеровская решетка). Благодаря этому минимизируется среднее расстояние для сбыта продукции или поездок в центры для покупок и обслуживания.

Теория В. Кристаллера объясняет, почему одни товары и услуги должны производиться (предоставляться) в каждом населенном пункте (продукты первой необходимости), другие — средних поселениях (обычная одежда, основные бытовые услуга и т.п.), третьи — только в крупных городах (предметы роскоши, театры, музеи и т.д.)

Каждое центральное место имеет тем большую зону сбыта, чем выше уровень иерархии, к которому оно принадлежит. Кроме продукции, необходимой для зоны своего ранга (своего шестиугольника), центр производит (предоставляет) товары и услуги, типичные для всех центров низших рангов.

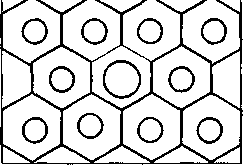
Рис. 3.5. Размещение зон обслуживания и населенных пунктов по теории В. Кристаллера

Тип иерархии определяется числом центральных мест данного уровня. Число подчиненных центральных мест, увеличенное на единицу, обозначается буквой К. Любой центр всегда имеет зависимое от него одинаковое количество поселений, занимающих более низкую ступень.

Рассмотрим, например, случай, когда имеется трехступенчатая иерархия поселений: город — поселок — деревня. Тогда при К = 7 вокруг каждого города будет расположено 6 поселков, а вокруг каждого поселка — 6 деревень, т.е. вокруг города будет всего 6 поселков и 36 деревень. При четырехступенчатой иерархии (город — поселок — поселение — деревня) вокруг города разместятся 6 поселков, 36 поселений и 216 деревень и т.д. Общая формула для отражения данной зависимости имеет следующий вид:

M_n =(K − 1)ⁿ ,

где M_n — число зависимых мест на той или иной степени иерархии; п — ступень иерархии.

Количество возможных типов иерархии в принципе может быть любым. Однако наибольшее внимание В. Кристаллер и его последователи уделяли анализу трех типов, или вариантов, иерархии при К = 3, 4, 7. Эти варианты иерархии систем расселения интерпретируются следующим образом.

Вариант при К = 3 обеспечивает оптимальную конфигурацию рыночных зон (территорий, население которых приобретает товары и услуги в данном центральном месте). Обслуживание территории достигается наименьшим возможным числом центральных мест. При этом каждое центральное место обслуживается тремя центральными местами следующего, более высокого уровня иерархии и находится на равных расстояниях от них.

Вариант при К = 4 создает наилучшие условия для строительства транспортных путей, так как в этом случае наибольшее число центральных мест будет расположено на одной трассе, соединяющей более крупные города, что обеспечит минимальные издержки на строительство дороги, т.е. данное центральное место будет находиться на кратчайшем расстоянии до двух ближайших центров более высокого уровня иерархии.

Вариант при К = 7 представляется целесообразным, если необходим четкий административный контроль. В этом случае все центральные места, зависимые от данного места, полностью входят в его зону.

Из приведенных примеров видно, что функции поселений различны, каждое их них имеет свой радиус влияния и притяжения. В соответствии с этим возможны и разные способы территориальной организации систем расселения, при которых создаются наиболее благоприятные условия для выполнения тех или иных их функций. Рассмотренные три случая, соответствующие значениям показателя К, можно интерпретировать как рыночную, транспортную и административную ориентации в формировании территориальной структуры расселения.

Теория центральных мест В. Кристаллера хотя и носит крайне абстрактный характер, но позволяет сформулировать общие представления о целесообразном расселении на той или иной территории. Ее можно рассматривать как теорию, дающую идеальный эталон системы расселения, с которым следует сравнить складывающиеся в реальности системы расселения с целью выявления направлений их совершенствования. Известны также примеры практического применения теории центральных мест к решению конкретных проблем территориальной организации хозяйства и расселения в различных странах.

3.5. Региональные рынки и пространственная теория цены

Многие учебники микроэкономики начинаются с анализ механизма спроса и предложения на товарном рынке, демонстрируя при этом модель рыночного равновесия, где предполагается, что спрос на товар D падает при увеличении цены Р, предложение товара S, наоборот, растет при увеличении цены (рис. 3.6). Пересечение обратных функций спроса и предложения Q^D = D(P) и Q^S = S(P) дает точку равновесия спроса и предложения Q* и цену равновесия Р*:

Q* = D (Р*) = S (Р*).

Приведенная широко известная модель имеет, однако, принципиальный недостаток: она игнорирует влияние пространства или (что по сути то же самое) допускает, что рынок является точкой. Для теории пространственной или региональной экономики такие предположения неприемлемы. По-видимому, первым, кто обратил внимание на это несоответствие (еще в 1838 г.), был французский экономист — математик О. Курно.

Начальный шаг анализа механизма спроса и предложения в экономическом пространстве — это рассмотрение пространственно разделенных автономных региональных рынков. Очевидно, что в каждом полностью автономном регионе будут устанавливаться свое рыночное равновесие спроса и предложения и свои цены рыночного равновесия, т.е. в каждом регионе описанная выше модель будет "работать" автономно.

Ситуация принципиально усложняется, если региональные рынки связываются друг с другом. Проведем анализ двух рынков региональной системы, производящей и потребляющей однородный товар.

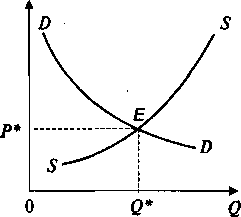
Рис. 3.6. Равновесие спроса и предложения однородного товара на точечном рынке

Пусть А₁ — цена равновесия для автономного региона 1; А₂— то же для автономного региона 2; Т_1,2 — транспортные затраты на доставку единицы товара из региона 1 в регион 2; Т_2,1— транспортные затраты на доставку единицы товара из региона 2 в регион 1. Задача состоит в том, чтобы определить объемы производства, межрегиональные поставки товара и цены равновесия (Р₁* и Р₂*) в системе связанных региональных рынков.

Пусть для определенности А₂ > А_1. Тогда у производителей (продавцов) возникает стимул для поставки товара из региона 1 в регион 2 с целью реализации его по более высокой цене. Последствие открытия региональных рынков будет зависеть от соотношения разницы А₂ — А₁ и транспортных затрат Т_1,2 .

Если оказывается, что А₂— А₁ < Т_1,2 ,то межрегиональная торговля неэффективна, поскольку выигрыш производителя (продавца) региона 1 на цене реализуемого товара меньше транспортных затрат. В этом случае состояние равновесия региональных рынков сохраняются такими же, как и при автономном их функционировании. Более интересен вариант, когда А₁ = А₂ . Тогда выгодно поставлять товар из региона 1 в регион 2, а на каждом региональном рынке установится новое равновесие. Цены равновесия будут удовлетворять условию Р₂* = Р₁* + Т_1,2 (причем Р₁* > А₁; Р₂* < А₂) ,а вывоз товара из региона 1 в регион 2 будет равен ввозу товара в регион 2 из региона 1 (с обратным знаком):

E_1,2 = E_{2,1 .}

Выведение условий рыночного равновесия для многорегиональной системы представляет собой принципиально более сложную математическую задачу. До создания мощных компьютеров и алгоритмов нахождения состояния равновесия в задачах большей размерности предпринимались попытки моделирования решений с помощью особых методик. В настоящее время решение таких задач не представляет чрезмерной сложности.

3.6. Теории региональной специализации и межрегиональной торговли

Теоретические принципы производственной специализации регионов и межрегиональной торговли формально (понятийно, терминологически) были впервые выведены в рамках теорий международных экономических отношений, т.е. международниками а не регионалистами. В связи с этим необходимо назвать классиков английской политической экономики А. Смита и Д. Рикардо и шведских экономистов Э. Хекшера и Б. Олина. Почему же полученные ими научные результаты правомерно относят к теоретическим основам региональной экономики? В гл. 1 мы отмечали наличие многих общих черт и проблем в межрегиональном и международном разделении труда, в межрегиональной и международной торговле, однако имеются и качественные различия.

Межрегиональное разделение труда и международная торговля — процессы, происходящие в рамках различных частей одной национальной зоны свободной торговли, одной таможенной территории, одной валютной системы, одного национального рынка труда и капитала. В межрегиональной торговле, как правило, отсутствуют административные, таможенные, политические, языковые и другие барьеры, в той или иной степени сохраняющиеся в международных экономических отношениях, несмотря на превалирующую тенденцию либерализации и глобализации.

Основные выводы международных теорий Смита — Рикардо и Хекшера — Олина получены в системе постулатов межрегиональных отношений, несмотря на то, что их авторы в своих поясняющих ситуациях упоминают об Англии, Шотландии, Португалии и приводят другие международные примеры. Безусловно, выводы, о которых идет речь, применимы и к международным отношениям (в большей степени это касается валютных и торговых союзов, общих рынков), но они требуют дополнений и корректировок, учитывающих специфику именно международных отношений (включение валютных, таможенных, институциональных и других условий). Б. Олин, лауреат Нобелевской премии, свою главную работу назвал "Межрегиональная и международная торговля" (1933 г.), подчеркивая общность и различия двух типов торговли.

Теория абсолютных и сравнительных преимуществ Смита — Рикардо

Названные классики политической экономии были идеологами свободной торговли (фритредерства), противостоящими сторонникам экономического меркантилизма. В этом отношении они, безусловно, родственны всем теоретикам региональной экономики. Международная (межрегиональная) торговля — способ получения выгоды для каждого участника. Международное разделение труда, полагал А. Смит, целесообразно осуществлять с учетом тех абсолютных преимуществ, которыми обладает та или иная страна (имеется в виду регион). Каждая страна (регион) должна специализироваться на производстве и продаже того товара, по которому она обладает абсолютным преимуществом. Если она сконцентрирует свои ресурсы на производстве только таких товаров и откажется от производства товаров, по которым страна (регион) не обладает абсолютными преимуществами, то это приведет к увеличению объемов производства и потребления товаров в сотрудничающих странах (регионах).

Рассмотрим условную ситуацию, когда два региона (А и В) производят два продукта (металл и хлеб) с разными трудовыми затратами.

В каждом регионе имеется по 10 единиц трудовых ресурсов, которые являются единственным ограничивающим фактором. При изолированном (автаркическом) функционировании регионы могут производить продукты в разных соотношениях, сообразуясь со своими внутренними потребностями. В частности, регион А может произвести 1 ед. металла и 5 ед. хлеба, регион В — 0,5 ед. металла и 4 ед. хлеба. Оба региона при этом полностью используют свои трудовые ресурсы.

Исходя из принципа абсолютных преимуществ региону А целесообразно специализироваться на производстве хлеба (разница издержек 1 - 2 = - 1), а региону В — на производстве металла (разница издержек 4 - 5 = - 1). Тогда регион А сможет произвести 10 ед. хлеба, а регион В — 2,5 ед. металла. При этом возникает множество вариантов обмена.

Допустим, оба региона намерены в результате специализации и обмена увеличить потребление обоих продуктов по сравнению с изолированным развитием. Пусть регион А из произведенных 10 ед. желает 5,2 ед. использовать внутри региона, а 4,8 ед. продать в обмен на металл. Регион В намерен из 2,5 ед. металла использовать у себя 1,3 ед., а 1,2 ед. обменять на хлеб. Очевидно, здесь возникает вопрос о ценах обмена. Один из компромиссов — справедливые цены, пропорциональные трудовым затратам на производство металла и хлеба, т.е. 4:1. В этом случае предлагаемые на продажу регионом А 4,8 ед. хлеба эквивалентны 1,2 ед. металла, предлагаемых регионом В.

В итоге в регионе А потребление составит: 1,2 ед. металла (+0,2) и 5,2 ед. хлеба (+0,2), в регионе В — 1,3 ед. металла (+0,8) и 4,8 ед. хлеба (+0,8). Существует достаточно широкий диапазон цен обмена, позволяющий обоим регионам получить выгоду от торговли.

Д. Рикардо продвинулся в теории существенно дальше А. Смита. Он доказал, что абсолютные преимущества представляют лишь частный случай общего принципа рационального разделения труда. Главное — не абсолютные, а относительные (сравнительные) преимущества. Даже страны (регионы), имеющие более высокие производственные издержки по всем товарам, могут выиграть от специализации и обмена благодаря игре, на разнице издержек.

Вернемся к предыдущему примеру. Вместо региона В введем в рассмотрение регион С, где издержки выше, чем в регионе А,по обоим товарам.

Если придерживаться принципа А. Смита, то торговля региона А с регионом С бессмысленна ("там все дороже"), а для региона С с регионом А безнадежна ("нашу дорогую продукцию не купят"). На самом деле это не так.

Сохраним все прежние условия по региону А. Регион С при изолированном развитии производит и потребляет 0,4 ед. металла и 3,8 ед. хлеба, он также располагает 10 ед. трудовых ресурсов.

Замечаем, что регионы А и С имеют существенно разные соотношения издержек. В регионе А металл дороже хлеба в 5 раз, а в регионе С — только в 3 раза. Таким образом, регион А имеет относительное (и абсолютное) преимущество по производству хлеба, а регион С — относительное (но не абсолютное) преимущество по производству металла. На использовании относительных преимуществ основаны рациональная специализация регионов и межрегиональная торговля.

Допустим, что в условиях разделения труда регион А будет производить 10 ед. хлеба, а регион С — 1²/з ед. металла (10 : 6 = 1²/з). Существует множество вариантов обмена, при которых оба региона, безусловно, выигрывают в том смысле, что могут увеличить внутреннее потребление обоих товаров по сравнению с автаркической ситуацией. Например:

Bариант 1. Регион А вывозит 4,6 ед. хлеба, регион С — 1²/9 ед. металла. В регионе А потребление составит: металла — 1²/9 (+²/9), хлеба — 5,4 (+0,4). В регионе С потребление составит: металла — ⁴/9[+ 0,04 (4)], хлеба — 4,6 (+0,8);

Bариант 2. Регион А вывозит 4,8 ед. хлеба, регион С — 1²/9 металла. Тогда потребление в регионе А:металла — 1²/9 (+¹/9), хлеба — 5,2 (+0,2). Потребление в регионе С: металла — ⁵/₉[+0,15 (5)], хлеба — 4,8 (+1,0).

Отметим, что обмен по ценам, пропорциональным региональным трудовым издержкам (6 : I),невыгоден для региона А. При таких ценах он в результате обмена не может получить выигрыш в потреблении по обоим продуктам.

Из анализа, проведенного Д. Рикардо, следуют два вывода:

1. выигрыш при обмене происходит не из абсолютного преимущества, а из того, что соотношения издержек в разных регионах различны;
2. производство и потребление всех товаров может быть увеличено, если регионы будут специализироваться на производстве и торговле теми товарами, по которым они обладают сравнительными преимуществами.

К сожалению, имеется масса свидетельств того, что обыденное экономическое мышление по-прежнему тяготеет к представлениям А. Смита, но не Д. Рикардо.

Теория Хекшера — Олина

В теориях А. Смита и Д. Рикардо главным фактором, определяющим рациональную структуру производства и обмена, являются трудовые издержки. В 30-х годах XX в. шведские экономисты Э. Хекшер и Б. Олин развили теорию международного (межрегионального) разделения труда, введя в рассмотрение соотношения основных взаимозаменяемых факторов производства (труда, капитала, земли и др.). Их основные теоретические положения сводятся к следующему:

1. страны (регионы) должны вывозить продукты интенсивного использования избыточных (относительно недефицитных) факторов производства и ввозить продукты интенсивного использования дефицитных для них факторов;
2. в международной (межрегиональной) торговле при соответствующих условиях осуществляется тенденция выравнивания факторных цен;
3. вывоз и ввоз товаров могут заменяться перемещением факторов производства.

Хекшер и Олин обосновывали целесообразность либерализации не только торговли, но и международного (межрегионального) перемещения факторов производства. Отметим снова, что в приведенных постулатах и выводах отсутствует какая-либо международная специфика. Эта теория находится полностью в рамках условий межрегиональных отношений, тем более что по сравнению с товарообменом перемещение труда и капитала между регионами одной страны встречает гораздо меньше препятствий, чем между разными странами.

Из выводов Хекшера и Олина следует, что отсталые или развивающиеся страны (регионы), имеющие, как правило, сильный дефицит капитала и избыток рабочей силы, должны специализироваться на производстве и вывозе трудоемкой продукции. Развитые страны (регионы), накопившие большие массы функционирующего капитала (в том числе научно-технического), должны стремиться к вывозу капиталоемкой продукции. Страны (регионы), обладающие большими площадями сельскохозяйственных угодий и относительно низкой плотностью населения, заинтересованы в расширении вывоза сельскохозяйственной продукции. Заметим, что земля и другие естественные ресурсы являются немобильными факторами, а перемещаться могут только продукты их использования.

Основные допущения и интерпретации теории Хекшера — Олина подвергались проверке и корректировке в последующие десятилетия. В частности, было установлено, что для выбора целесообразной структуры вывоза и ввоза товаров необходимо принимать во внимание не только прямые затраты производственных факторов, но и косвенные, сконцентрированные в потребляемых сырье и материалах. Эту аналитическую задачу реализовал много позже В. Леонтьев на основе метода межотраслевого баланса (input-output analysis). Полученные им результаты вошли в историю как парадокс В. Леонтьева.

Контрольные вопросы

1. Что лежит в основе теории сельскохозяйственного штандорта Й. Тюнена?
2. В чем сущность рационального штандорта промышленного предприятия В. Лунхардта?
3. Какова основа теории промышленного штандорта А. Вебера?
4. В чем состоят особенности теории центральных мест?
5. Какие критерии взяты за основу в теориях региональной специализации и межрегиональной торговли?
6. Кто считается основоположником общей теории размещения?

Главная     Каталог раздела     Предыдущая     Оглавление     Следующая     Скачать в zip